ARC-Flow : Articulated, Resolution-Agnostic, Correspondence-Free Matching and Interpolation of 3D Shapes Under Flow Fields

Adam Hartshorne
University of Bath
Allen Paul
University of Bath
Tony Shardlow
University of Bath
Neill D.F. Campbell
University of Bath

This work presents a unified framework for the unsupervised prediction of physically plausible interpolations between two 3D articulated shapes and the automatic estimation of dense correspondence between them. Interpolation is modelled as a diffeomorphic transformation using a smooth, time-varying flow field governed by Neural Ordinary Differential Equations (ODEs). This ensures topological consistency and non-intersecting trajectories while accommodating hard constraints, such as volume preservation, and soft constraints, e.g. physical priors.

Correspondence is recovered using an efficient Varifold formulation, that is effective on high-fidelity surfaces with differing parameterisations. By providing a simple skeleton for the source shape only, we impose physically motivated constraints on the deformation field and resolve symmetric ambiguities. This is achieved without relying on skinning weights or any prior knowledge of the skeleton's target pose configuration. Qualitative and quantitative results demonstrate competitive or superior performance over existing state-of-the-art approaches in both shape correspondence and interpolation tasks across standard datasets.

Physically Plausible Shape Interpolation without Correspondence

The goal is correspondence-free matching and interpolation between articulated shapes (i.e. pose variation rather than between two identities). We do not assume a shared triangulation between the two shapes so there can be differences in resolution, etc..

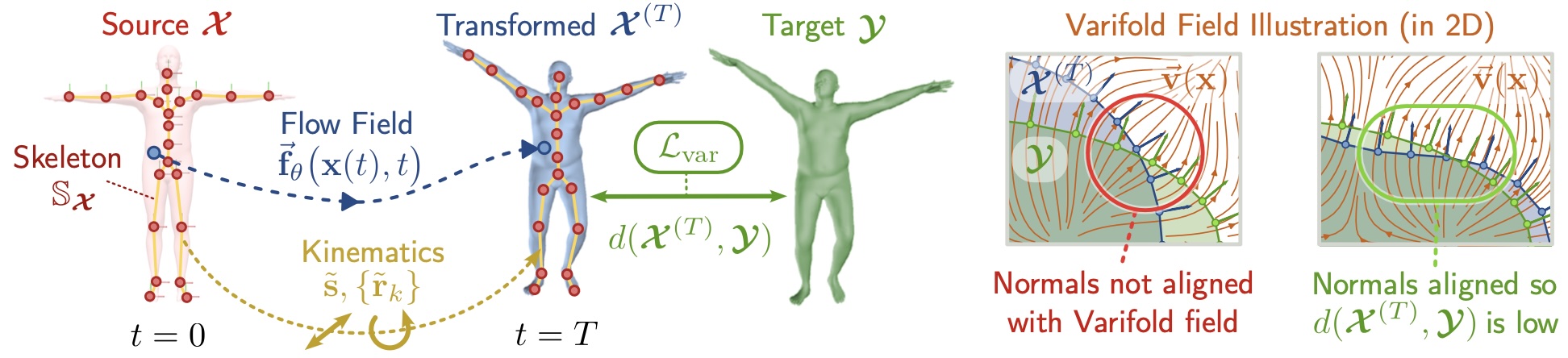
We use a “Varifold” matching metric from geometric measure theory. Whilst a direct implementation would yield a quadratic matching complexity in the number of vertices, we demonstrate that our new compression approach allows us to hugely reduce the complexity with minimal impact on matching performance.

...
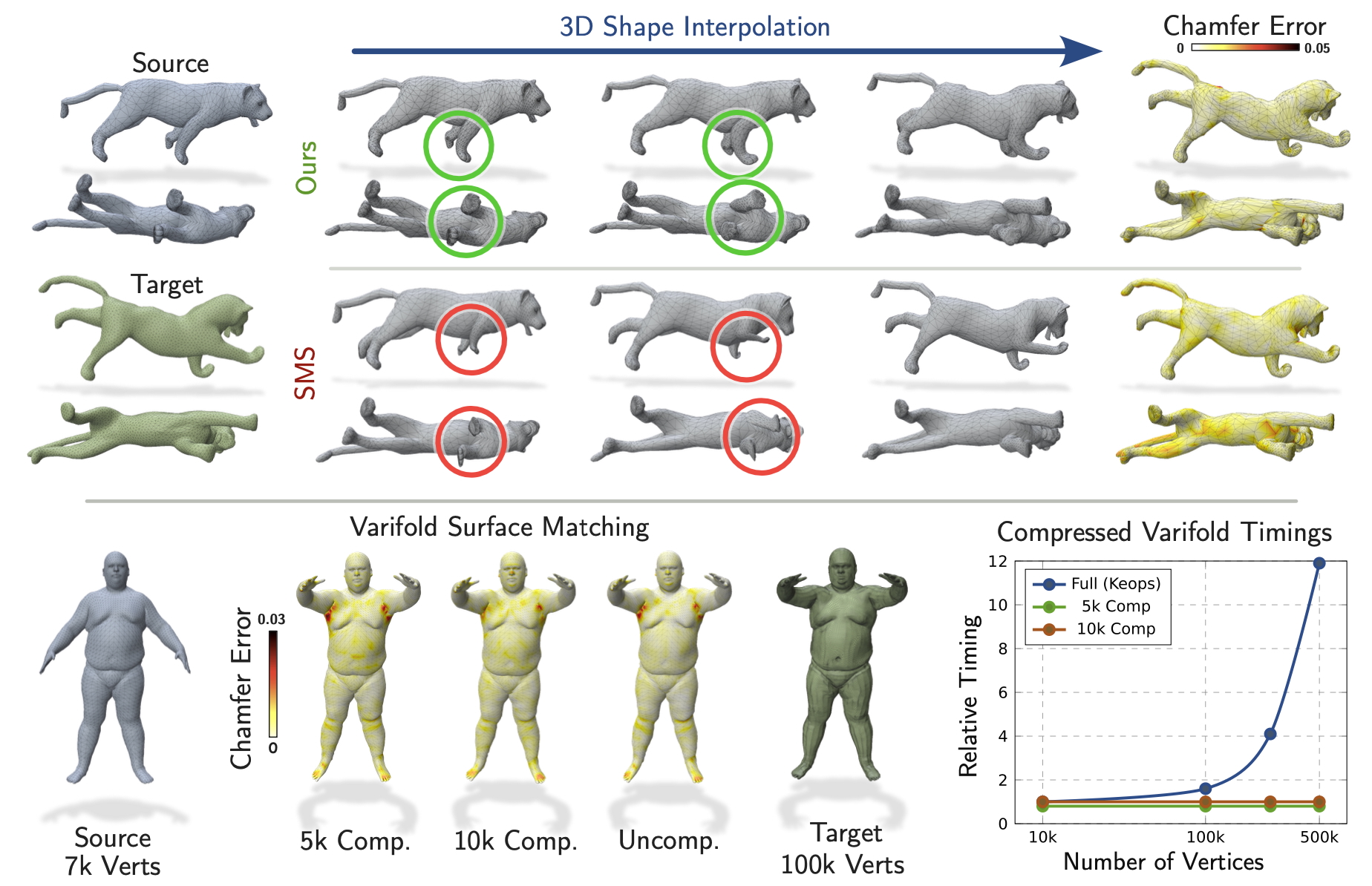
Top: 3D shape interpolation. Our method obtains a more reliable interpolation than existing state-of-the-art approaches (e.g. Spectral Meets Spatial) even under substantial non-isometric deformation. Samples taken at t = {0.25, 0.5, 0.75, 1.0} along the deformation path. Bottom: Scaling to high-resolution meshes. Using Varifold compression we obtain dramatic computational savings, while maintaining similar perceptual quality, allowing us to scale to high resolution meshes.

Approach

The method comprises four key points:

  1. Deformation via a diffeomorphic flow field to guarantee preservation of topology; the vector field is constructed to be divergence free and therefore preserves volume.

  2. A varifold metric is used to ensure the deformed surface matches the target without known correspondence.

  3. We supply the source with a simple, articulated internal skeleton and then force our field to infer the new skeletal pose automatically whilst promoting local rigidity.

  4. The surface and soft tissue surrounding the skeleton are encouraged to deform in a conformal manner by incorporating physically inspired priors.

...
Left: Method overview. We transform the source shape to match the target using a diffeomorphic differential vector field; we also recover the forward kinematic transformation of the source skeleton. Matching is performed with a correspondence-free Varifold metric. Right: Varifold field. Visualisation of an implicit Varifold field for intuition; explict computation of the vector field is not required for matching.

Results

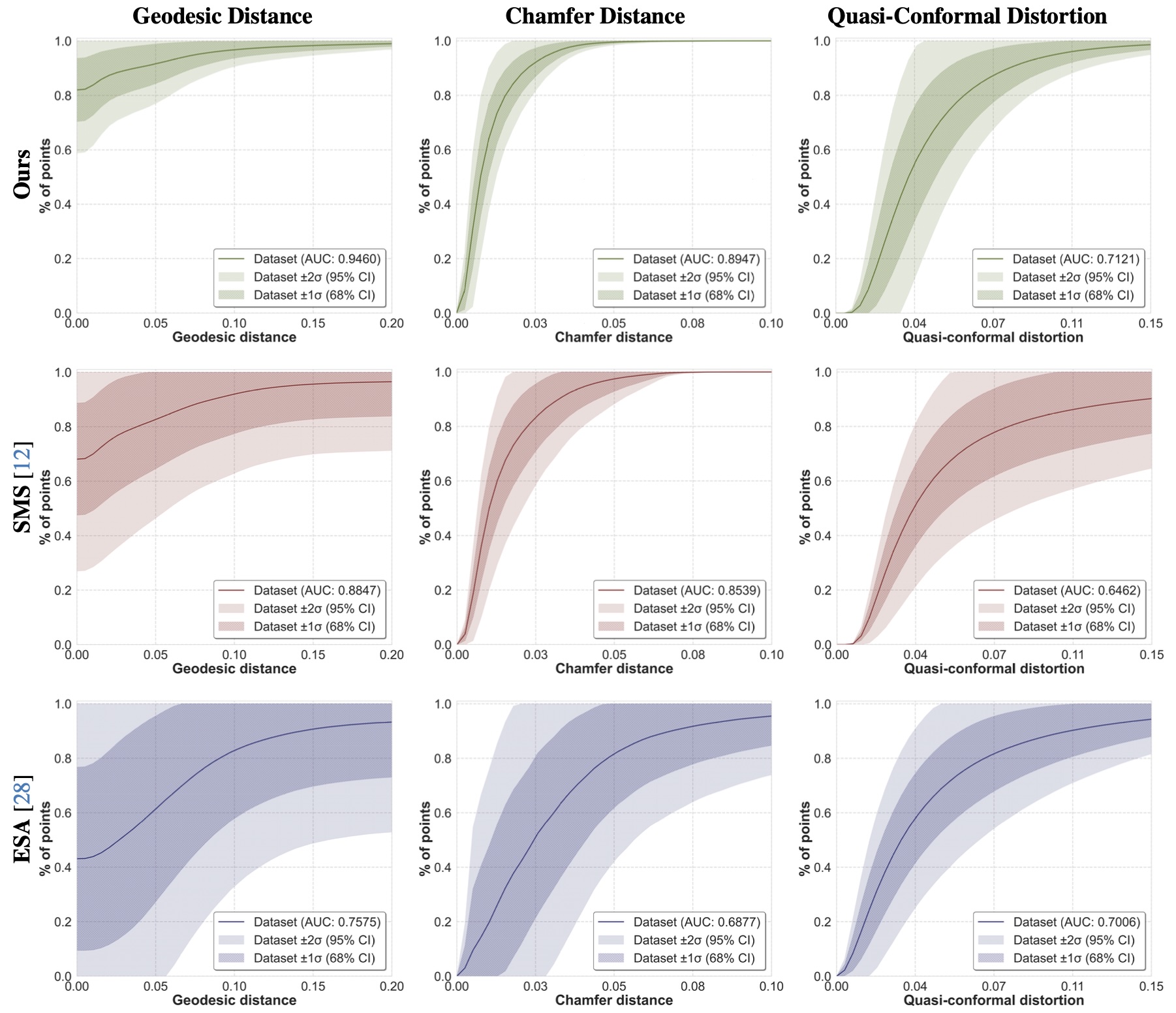
We show improved performance on three metrics:

We also improve over methods where the correspondence is given and where large datasets are used for training; we require neither but we do need a simple skeleton to be provided for only the source shape. Further details are given in the paper.

...
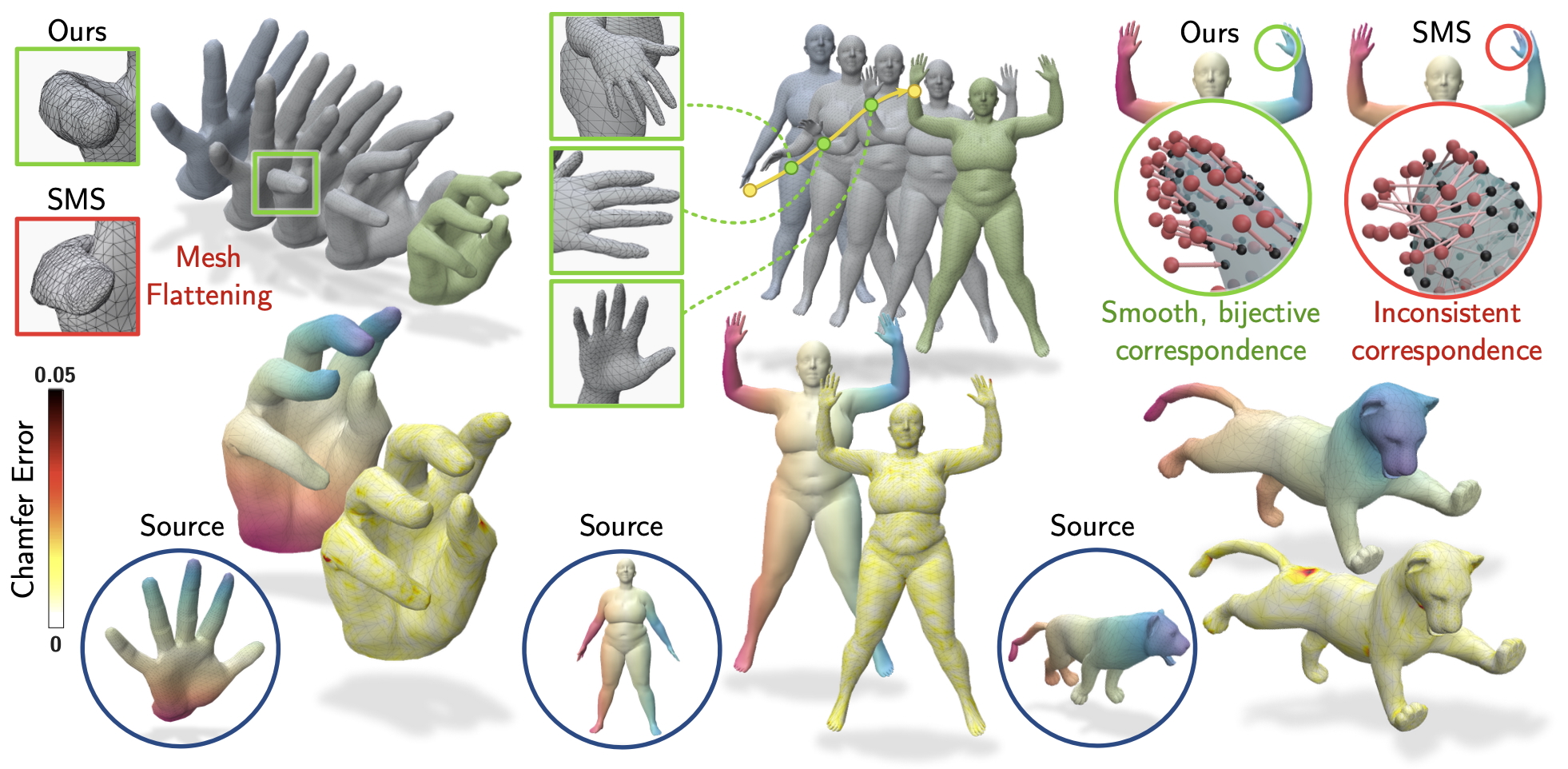
Interpolation results for DFAUST. Ours vs SMS and ESA. Mean and confidence intervals for the three metrics are shown; top row has our results, middle SMS & bottom row ESA.

We show illustrations of challenging examples from three standard datasets: FAUST, MANO and SMAL.

...
Challenging examples from each dataset. Top Left: Sample interpolations. Even under large deformations, we do not suffer from flattening or "rubber hand" syndrome due to the articulated structure and the soft tissue priors. Top Right: Correspondence detail. We guarantee smooth, bijective correspondences by construction in contrast to inconsistent correspondences from permutation matrices. Bottom: Correspondence and chamfer distances. Accurate correspondences are recovered with low chamfer errors.

BMVA Symposium on 3D Vision Keynote Talk

Slides from a keynote talk entitled “A Hitchhiker’s Guide to Diffeomorphisms, Hamiltonian Flows and Geometric Measure Theory” at the BMVA Symposium on 3D Vision are available here.

Code

Code will be made available shortly.

Publications

3dv25_arc_flow
ARC-Flow : Articulated, Resolution-Agnostic, Correspondence-Free Matching and Interpolation of 3D Shapes Under Flow Fields,
Adam Hartshorne, Allen Paul, Tony Shardlow and Neill D. F. Campbell,
International Conference on 3D Vision (3DV), 2025
[pdf]
currents_varifolds_compression
Sparse Nystrom Approximation of Currents and Varifolds,
Allen Paul, Neill D. F. Campbell and Tony Shardlow,
arXiv e-print, 2024
[pdf] [arXiv link]

Acknowledgements

We are grateful for support from the EPSRC SAMBa Centre for Doctoral Training in Statistical Applied Mathematics (EP/L015684/1), the EPSRC CAMERA Research Centre (EP/M023281/1 and EP/T022523/1), UKRI Strength in Places Fund MyWorld Project (SIPF00006/1) and the Royal Society.