Learning Alignments
Overview
This project encompasses a series of work on composite models with applications to the temporal alignment of sequences; our aim is to automatically learn alignments between high-dimensional data in an unsupervised manner. Our proposed methods cast alignment learning in a framework where both alignment and data are modelled simultaneously. Further, we automatically infer groupings of different types of sequences within the same dataset. We derive probabilistic models built on non-parametric priors that allow for flexible warps while at the same time providing means to specify interpretable constraints.
Given a set of time series sequences, the temporal alignment task consists of finding monotonic warps of the inputs (which typically correspond to time) that remove the differences in the timing of the observations. There are three intrinsic sources of ambiguity in this problem that motivate the use of probabilistic modelling. Firstly, the temporal alignment problem is ill-posed: there are infinitely many ways to align a finite set of sequences and we’d like to model this warping uncertainty. Secondly, the observed sequences might correspond to multiple different unknown underlying functions, hence the assignment of sequences to groups is ambiguous. Furthermore, the observed sequences are often noisy, requiring a principled way to model the observational noise. We introduce a non-parametric probabilistic model of monotonic warps and model each sequence as a composition of such a warp and a standard GP. To allow for alignment in multiple groups and to find these groups in an unsupervised manner, we use probabilistic alignment objectives (such as GP-LVM or DPMM).
Results
We demonstrate the efficacy of our approach with superior quantitative performance to the state-of-the-art approaches and provide examples to illustrate the versatility of our model in automatic inference of sequence groupings, absent from previous approaches, as well as easy specification of high level priors for different modalities of data.
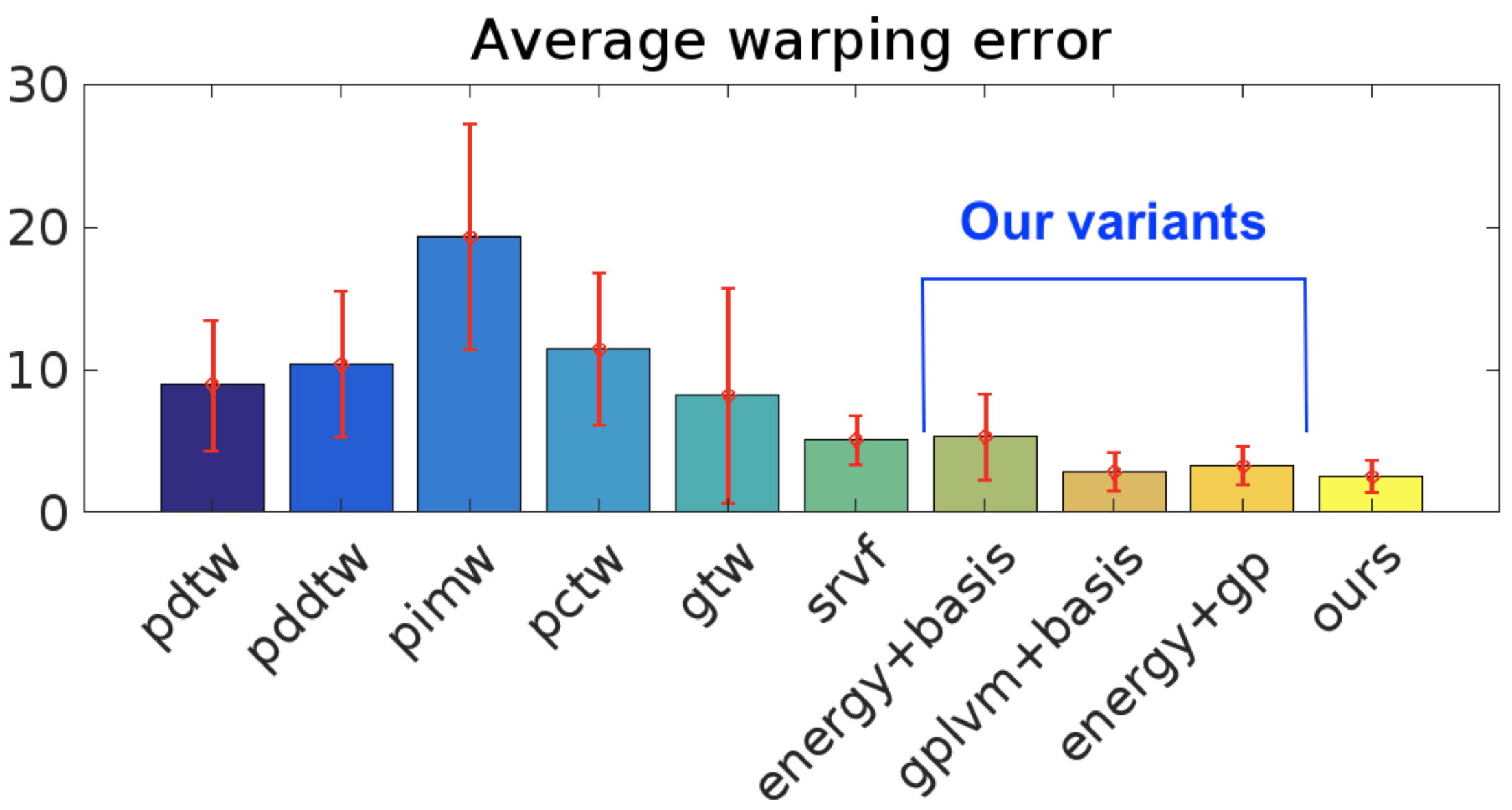
| MSE (SD) | SRVF | GP-LVM+BASIS | OURS |
|---|---|---|---|
| Alignment | 6.4 (±1.7) | 8.4 (±2.7) | 5.9 (±1.1) |
| Warping | 30.0 (±10.4) | 9.7 (±4.9) | 9.7 (±5.7) |
The following diagram illustrates the results of our two methods for automatic alignment and clustering of signals, one using the GP-LVM and the other using an explicit Dirichlet Process clustering model. The later is more appropriate for the heart beats data since we are informed by clinicians that the data should be grouped into distinct patterns.
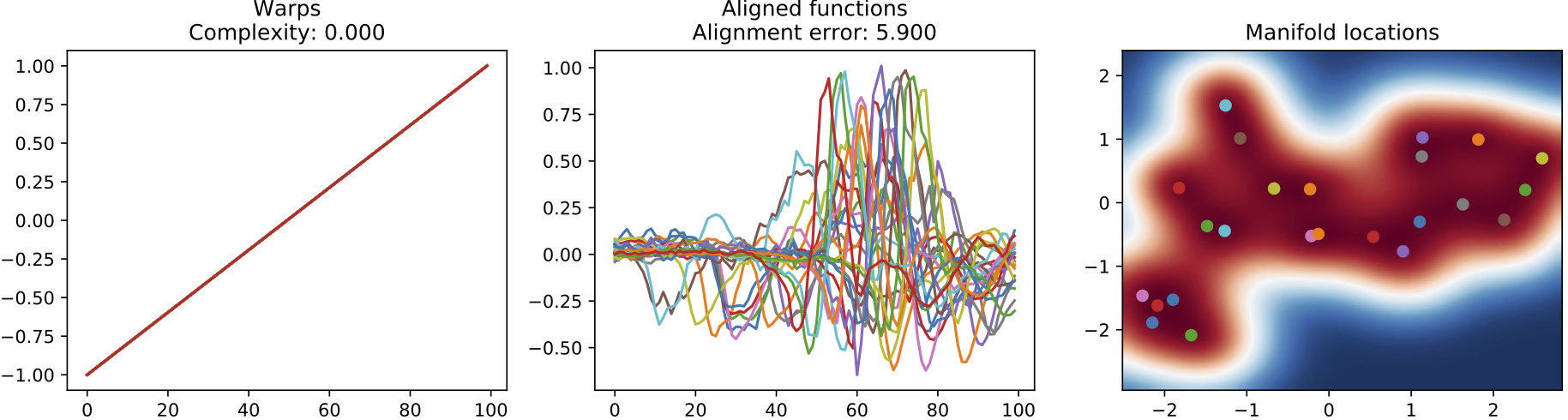
(a) Input sequences. The corresponding clustering does not discover the two different types of heartbeats.
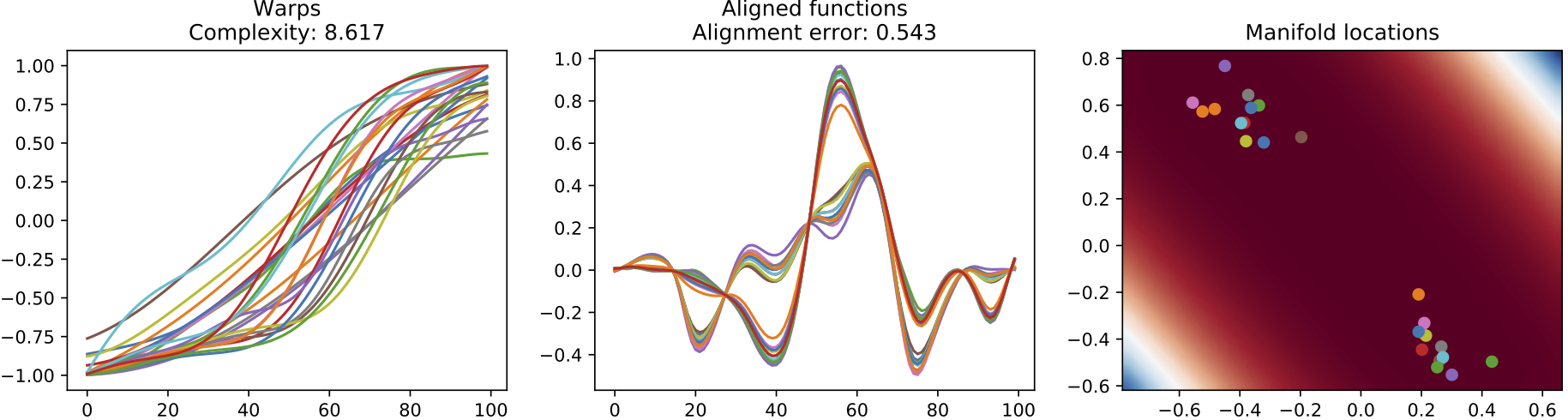
(b) Warps, resulting alignment and the manifold for the results of the GP-LVM alignment approach.
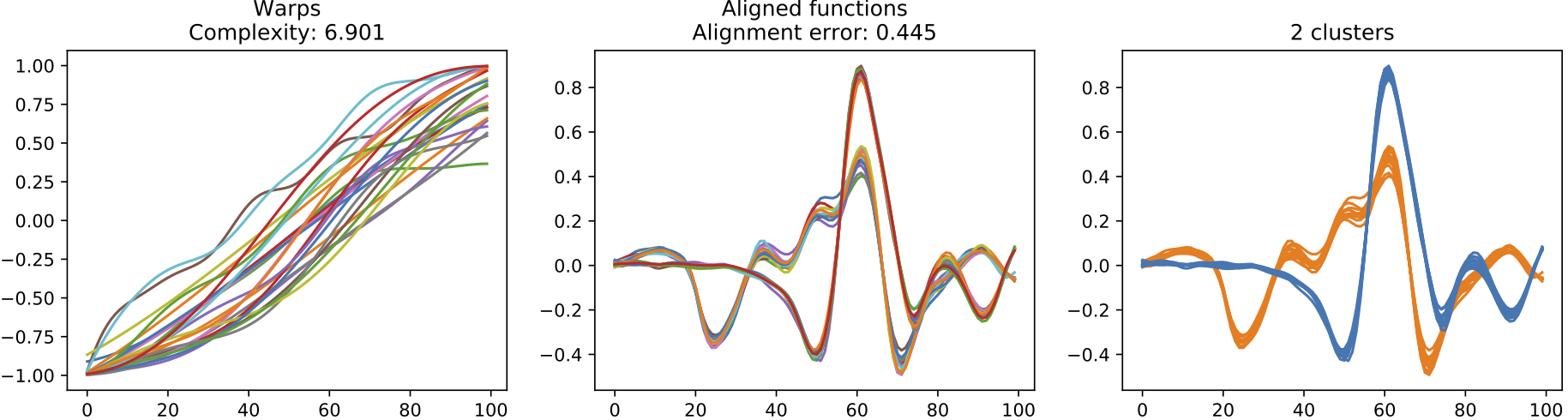
(c) Warps, resulting alignment and the clustering discovered for the results of the Dirichlet Process alignment approach.
Publications
Ivan Ustyuzhaninov, Ieva Kazlauskaite, Markus Kaiser, Erik Bodin, Neill D. F. Campbell and Carl Henrik Ek,
Conf. on Uncertainty in Artificial Intelligence (UAI), 2020
[pdf] [supplemental] [code]
Ieva Kazlauskaite, Ivan Ustyuzhaninov, Carl Henrik Ek and Neill D. F. Campbell,
NeurIPS Workshop on Bayesian Non-Parametrics, 2018
[pdf]
Ieva Kazlauskaite, Carl Henrik Ek and Neill D. F. Campbell,
NeurIPS Workshop on Learning in High-Dimensions with Structure, 2016
[pdf]
Acknowledgements
This work has been supported by EPSRC CDE (EP/L016540/1) and CAMERA (EP/M023281/1) grants as well as the Royal Society. IK would like to thank the Frostbite Physics team at EA.
